Một trong những chăm đề luôn luôn phải có đóng một mục đích rất là quan trọng vào kỳ thi Đại học - THPT Quốc Gia môn Toán thù kia chính là khảo sát điều tra và vẽ thứ thị hàm số, trong số ấy bao gồm phần xét tính 1-1 điệu của hàm số là một phần tương đối tốt với khó khăn.Tài liệu bao gồm bắt tắt lại phương thức một bí quyết cô ứ đọng tốt nhất cùng phần bài tập có lời giải kèm theo nhằm luyện thêm
CHỦ ĐỀ 1: SỰ BIẾN THIÊN CỦA HÀM SỐ
Bài toán: Xét sự phát triển thành thiên của hàm số y = f(x).
Bạn đang đọc: Bài tập xét tính đơn điệu của hàm số
Phương pháp : Ta đề xuất triển khai công việc sau:
Cách 1: Tìm miền xác định của hàm số.
Bước 2: Tính đạo hàm f ’(x), rồi giải pmùi hương trình f ‘(x) = 0.
Bước 3: Lập bảng thay đổi thiên của hàm số.
Bước 4: tóm lại.
Những bài tập ôn luyện: Khảo tiếp giáp chiều phát triển thành thiên của những hàm số.
Tìm những khoảng tầm đồng biến chuyển, nghịch trở thành của hàm số.
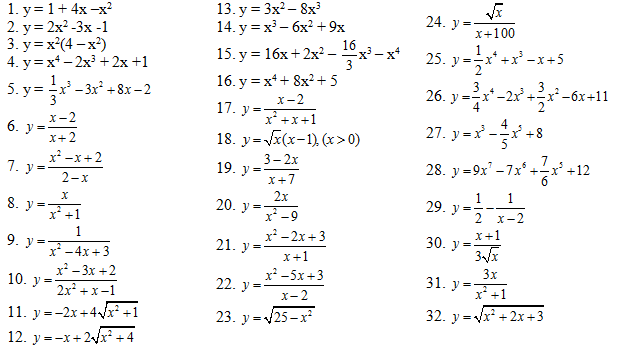
CHỦ ĐỀ 2: SỰ BIẾN THIÊN CỦA HÀM SỐ TRÊN MỘT MIỀN. Xem thêm: Ngọc Anh Kể Về Cảnh Táo Bạo Bị Cắt Ở Phim Chàng Dâng Cá, Nàng Ăn Hoa!
Bài toán: Xác định m nhằm hàm số y = f(x, m) đồng biến đổi (hay nghịch biến) trên khoảng chừng I.
Phương pháp: Ta nên tiến hành các bước sau:
B1: Tìm miền xác định của hàm số.
B2: Tính đạo hàm f ‘(x).
B3: Lập luận cho các trường đúng theo (giống như đến tính nghịch biến) nhỏng sau:
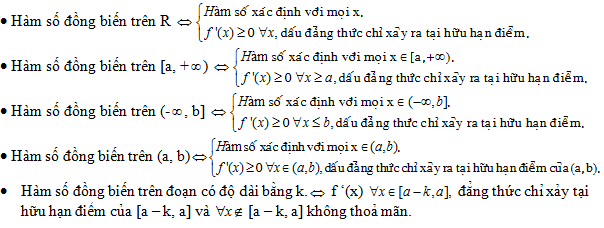
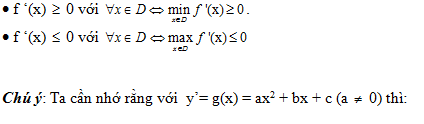



Bài 1: Tìm m sau cho hàm số:
1. y = mx3 – (2m – 1)x2 + (m – 2)x – 2 luôn đồng vươn lên là.
2. y = x3 + 3x2 + (m + 1)x + 4m nghịch phát triển thành trong (-1; 1). Đs:
3. y = (mét vuông + 5m)x3 + 6mx2 + 6x – 6 1-1 điệu trên R.
4. y = x3 – 3(m – 1)x2 + 3m(m-2)x + 1 hàm số đồng biến chuyển bên trên R.
5. y = x4 – 2mx2 + 2m + m4 luôn luôn đồng đổi thay.

Tải về
Luyện các bài luyện tập trắc nghiệm môn Tân oán lớp 12 - Xem ngay






